gacco 「統計学Ⅰ：データ分析の基礎」のまとめ

社会経済的な分野から理系的な分野へと応用分野が拡大
- 遺伝法則と生物測定（メンデル、ゴルトン、カール・ピアソン）
- 相関、回帰分析
実験計画法
- 統計的品質管理
数理統計学の確立
- 「科学の文法」（カール・ピアソン）
- 数理統計学の創始（R. A. フィッシャー）
  - 小標本理論、推測統計学、実験計画法、最尤法などを創始
近年はコンピュータの発展によりあらゆる分野へ

1-4. データ分析の流れ

データ分析のPDCAサイクル
- 何が知りたいかを考え、データを取り、統計的手法で解釈し、データに基づいて行動

BMI (Body Mass Index)
- BMI ＝体重(kg) ÷ 身長(m)の二乗
- 基準値は22
- 25以上で肥満
- 根拠はアメリカにおける疫学調査
国勢調査
- 人口推計や他の統計調査の基礎資料として利用される

1-5. データの種類

質的データと量的データ
質的データ
- 数量として意味のないもの
- 順序尺度：順序に意味があるもの（例）大変良い、やや良い、等
- 名義尺度：順序にも意味のないもの（例）性別、職業
量的データ
- 連続 or 離散
- 比例尺度 or 間隔尺度
  - 比例尺度：○倍に意味のあるもの（例）長さ
  - 間隔尺度：○倍に意味のないもの（例）温度
- 国勢調査等では、回答者が答えやすいようにコード化されている場合も
健康診断の多くの検査項目の基準値は、健康な人の95％が入る範囲とされている

1-6. データセットの例

スプレッドシートの表では通常、行を「個体」、列を「項目（変数）」とする
n を「データの大きさ」あるいは「標本の大きさ」と呼ぶ
- 統計学では「標本数」は誤用

1-7. データから情報を得る

度数分布表や円グラフを作成すると、分布の様子がよく理解できる
平均や標準偏差を計算すると、データの性質や分布がよく理解できる

Week2: 統計グラフと質的データの要約

下川敏雄氏（山梨大学大学院医学工学総合研究部　准教授）

2-1. 度数分布表による要約

新製品

	度数	相対度数
美味しい	158	0.380
やや美味しい	133	0.320
どちらでもない	42	0.101
やや不味い	50	0.120
不味い	33	0.079

清涼飲料水メーカーA社が行った官能検査のデータ例
度数・・・質的変数の項目に該当する個体の数
相対度数・・・個体の割合
「美味しい」から「不味い」までの段階評価は、順序尺度
- 順序があるので、項目を入れ替えできない
名義尺度では、度数で並べ替えを行った方が解釈しやすい
度数分布表は、棒グラフ、円グラフ、帯グラフ、（集合）棒グラフの基礎となる

2-2. 統計グラフ(1) -円グラフと棒グラフ-

項目の内訳（構成比）を省察・・・円グラフ
項目間の度数の大小を比較・・・棒グラフ
- 棒グラフは「統計で嘘をつく方法の代名詞」（諸刃の剣）

2-3. 統計グラフ(2) - 帯グラフとまとめ-

複数の群での項目の構成比を省察・・・帯グラフ
- （例）「美味しい」あるいは「やや美味しい」というポジティブな回答をした割合はどのくらいか？
統計グラフ（統計的視覚表現）の目標
- データを分析する（データの表層を捉え、傾向を示唆できるか否かを精査する）
- 分析結果を伝える
「世界の富」
- 世界の裕福な20％の人々が世界の80％の富を独占（Paretoの法則）
- シャンパングラス視覚効果

2-4. 2変数のデータのまとめ方：クロス集計表

2変数の質的データの関係性を評価・・・クロス集計表（分割表）
行周辺度数・・・行単位での小計
列周辺度数・・・列単位での小計
全体度数（総度数）
「（行の数）×（列の数）のクロス集計表」と呼ばれる
行パーセント・・・行列周辺度数を100％に合わせたもの
列パーセント・・・列周辺度数を100％に合わせたもの
総（全体）パーセント

2-5. クロス集計表における諸種の測度

クロス集計表を作成する目的は
- 因果関係を評価する
- 連関関係を評価する
因果関係
- 因果関係がある2変数のクロス集計表では、原因を列側、結果を行側に書くのが一般的
  - 原因側の変数・・・説明変数（独立変数）
  - 結果側の変数・・・応答変数（従属変数）
  - 行パーセント、およびオッズ比で評価
連関関係
- 2変数に双方向の関係性があることを「連関関係」という
- 行パーセント、列パーセントの両方で解釈が可能
オッズとは、ある結果が生じる比率とある結果が生じない比率との比
オッズ比は、結果に対してどれくらい要因が寄与しているかを表わす

オッズ比の定義： ${ \displaystyle OR=\frac{a \times d}{b \times c} }$ 　（対角の積の比）

ファイ係数
- 連関関係を表わす測度
- 2個の質的変数の連関（相関）の強さを数値化した指標
- -1から1までの範囲の値を取る（負の連関＝-1.0、正の連関＝1.0、無関係＝0）

ピアソンの積率相関係数を2×2のクロス集計表に適用したものとしてのファイ係数も定義されており、これを特に四分点相関係数（four-fold point correlation coefficient）とも言う。-1≦φ≦1の値をとり、以下の式で表される。
${ \displaystyle \phi=\frac{adーbc}{\sqrt{r_{1} \times r_{2} \times c_{1} \times c_{2}}} }$

${B_{1}}$ ${B_{2}}$ 計

${A_{1}}$ a b ${r_{1}}$

${A_{2}}$ c d ${r_{2}}$

計 ${c_{1}}$ ${c_{2}}$ n

「ファイ係数（φ係数） | 統計WEB | 統計用語集」より

ファイ係数の目安
- 0.8 ≦ |φ| ・・・非常に強い関連
- 0.5 ≦ |φ| ＜ 0.8・・・やや強い関連
- 0.25 ≦ |φ| ＜ 0.5・・・やや弱い関連
- |φ| ≦ 0.25 ・・・非常に弱い関連（関連性なし）

2-6. 多重クロス集計表

3変数以上の質的変数（例えば、性別・自動車保持・自動車嗜好）の相互の連関関係を考察するための手法が「多重クロス集計表」
- 3変数の場合は「3重クロス集計表」
多重クロス集計表の作成手順
1. 性別でデータを二つに分ける（層化）
2. それぞれの性別でクロス集計表を作成する
3. 2個のクロス集計表を縦に並べる

性別	自動車保持	自動車嗜好		計
性別	自動車保持	好き	好きでない	計
男性	持っている	283	28	311
	持っていない	141	68	209
	計	424	96	520
女性	持っている	70	50	120
	持っていない	93	121	214
	計	163	171	334

多重クロス集計表の問題としてよく知られているのが、Simpsonのパラドックス
- 層化の前後で結果が逆転する
- 一般的には、多重クロス集計表ではそれぞれの層で解釈するのがよい

2-7. 多重クロス集計表における第3の変数

擬似的な関係（見かけの連関関係）
- 原因と結果それぞれに対して影響を与える「第3の変数」が存在
- 例えば、「血圧」「年収」に対する、第3の変数「年齢」
- 「血圧」と「年収」には連関関係はなく、「年齢」が「血圧」と「年齢」それぞれに影響を及ぼしている
媒介的な関係
- 原因と結果の間に媒介となる「第3の変数」が存在
- 例えば、「性別」「自動車事故経験」に対する、第3の変数「走行距離」
- 男性の方が「走行距離」が長い傾向にあり、その結果として「走行距離」が長いと「自動車事故経験」の割合が高くなった
交互作用
- 2つの変数間の連関パターンが「第3の変数」によって異なる

2-8. クロス集計表を用いた実践例

変数のコントロール（第3の変数の影響を減らす方法）
- 1. 調査方法によるコントロール
  - 調査段階で、第3の変数で層化したときの被験者数の割合ができるだけ等しくなるように被験者を集める（層別）
- 2. サブグループ解析
  - 層に対して個々にクロス集計表を作る（多重クロス集計表）
- 3. 数理的に調整
  - 多変量解析

層別化

ランダム化比較試験において、いずれかの群に特定の因子保有者が偏らないように、ランダム化前に、あらかじめ両群にこれらが均等に分かれるように操作すること。

「臨床試験の基礎知識 p.1」より

Week3: 量的データの要約

酒折文武氏（中央大学理工学部数学科　准教授）

3-1. 量的データの要約事始め

データの散らばりをグラフで表現する
- ドットプロット
- 幹葉図（みきはず／かんようず）
- ただし、個体が多い場合には不便
データの散らばりを大まかに把握する
- ヒストグラム
- 箱ひげ図
  - 複数のグループを比較するのに便利

3-2. 度数分布表とヒストグラム

度数分布表
- 階級に分けて、階級ごとに個体数や割合をまとめた表
- 階級幅
- 階級値（階級の中央の値）
度数分布表をグラフ化したものが、ヒストグラム、および度数折れ線
複数のグループを比較する場合は、縦軸は相対度数（あるいは密度）とするとよい
度数折れ線は、ヒストグラムの柱の真ん中を折れ線でつないだもの
- 複数のグループを重ねて描くときは、度数折れ線の方が見やすい
データが離散量の場合は、棒を線で描くか、棒の間隔を空けるようにする
- ただし、複数の離散値を1つの階級にまとめた場合（例：10～15点）には、間隔を空けずに柱で描くことも多い
階級数の工夫
- 境界を区切りのよい数字にする
- いくつか作成してみて、見やすいものを採用
- スタージェスの公式が参考になる場合もある

スタージェスの公式
${ \displaystyle k\simeq1+\log_{2}n }$

3-3. 分布を読みとる

ヒストグラムの読み取り方
- 単峰か多峰か
- 特に、山が1つで左右対称の形を「ベル型の分布」という
- 間欠泉のデータは多峰型
異質なデータの混在に注意
- 高原型（位置の近い複数のグループが混ざっている？）
- 離島（外れ値）
歪んだ分布
- 右に歪んだ（右の裾が長い）分布

3-4. 箱ひげ図

箱の左側、真ん中の線、右側はそれぞれ、第1四分位数、第2四分位数（中央値）、第3四分位数を示す
テューキーの箱ひげ図
- 一番有名な描き方だが、少し複雑
- 1. 四分位範囲（IQR）の長さを測る
- 2. 箱の端から四分位範囲の長さの1.5倍の位置に「フェンス」を作る
- 3. フェンスの内側にあるデータの中で最もフェンスに近いものまでヒゲをのばす
- 4. フェンスを越えたデータは外れ値として○で示す
- 5. フェンスからさらに四分位範囲の1.5倍を越えたものは「異常値」と呼ばれる
シンプルな箱ひげ図では、ひげは「最小値」「最大値」を表す
- 五数要約をグラフ化したものと捉えることができる
コンパクトなグラフなので、複数の分布を比較しやすい
- フィッシャーのアヤメのデータ（3種類のアヤメのがくの長さ）

がくの長さのばらつきをテューキーの箱ひげ図で比較（アヤメのデータより）

> boxplot(Sepal.Length ~ Species, data=iris, style="tukey")

f:id:akiyoko:20141229171518p:plain

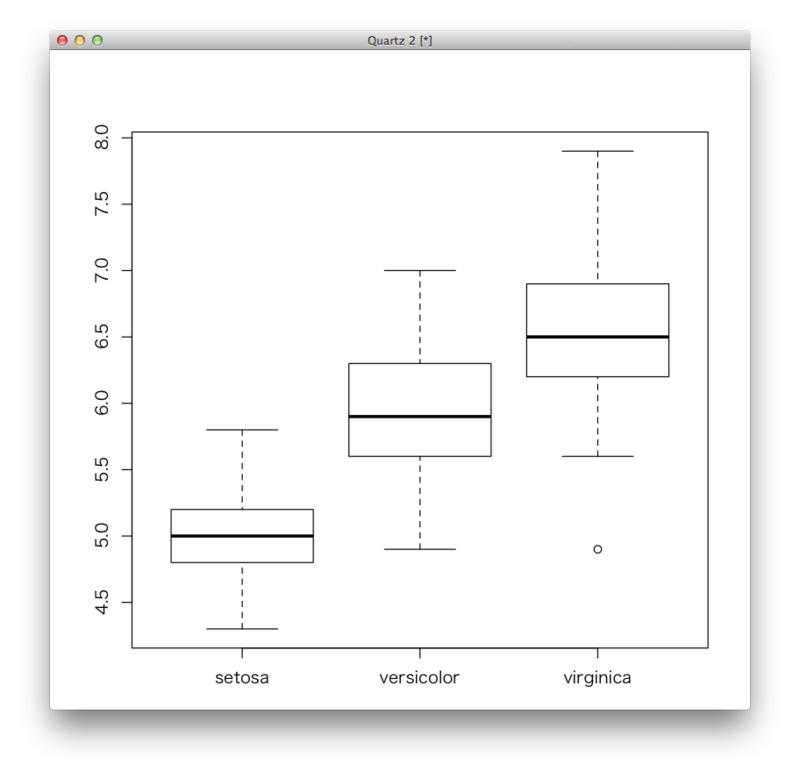
（参考）

3-5. 分布の位置を表す代表値

代表値
- 平均値（算術平均）
- 中央値
- 最頻値
- 連続する量的データの場合は、度数分布において最も度数の多い階級の階級値を「最頻値」とする
ベル型の分布では、平均≒中央値≒最頻値
右に歪んだ分布では、最頻値＜中央値＜平均
左に歪んだ分布では、平均＜中央値＜最頻値

3-6. 分布のばらつきの大きさを測る

ばらつきの大きさを測る指標
- 範囲・・・最大値－最小値
- 四分位範囲(IQR) ・・・第3四分位数－第1四分位数
- 分散・・・偏差を2乗して平均したもの
- 標準偏差・・・分散の平方根
分散には、n ではなく n-1 で割った分散が用いられることもある
- ${s^2}$ ・・・データを要約する場合に用いられることが多い
- ${u^2}$ （n-1で割ったもの）・・・統計的推測で用いられることが多い
変動係数

${ \displaystyle CV(\%)=\frac{標準偏差}{平均} }$

その他の指標
- 歪度（わいど）
- 尖度（せんど）

3-7. 標準偏差の活用

ベル型（正規分布）に近い分布の場合、「平均から標準偏差（シグマ）いくつ分離れているか」で、データの散らばりや相対的な位置を大雑把に把握できる
- 1シグマ・・・68％
- 2シグマ・・・95.4％
- 3シグマ・・・99.7％

標準得点＝(個体の値－平均)÷標準偏差
偏差値＝標準得点×10＋50

知能指数は、平均100、標準偏差15になるように作られている（ウェクスラー式）
管理図
- データが取られる工程に異常がないかをチェックする
- 中心線から±3シグマの範囲を超えていないかどうかを管理する

3-8. 格差を測る

格差を統計的に測るための方法
ローレンツ曲線
- 世帯数の累積相対度数と年間収入の累積相対度数を縦横軸にとって線でつないで視覚化したもの
ジニ係数
- 均等分布線とローレンツ曲線で囲まれた部分の面積の2倍
- 大きいほど格差が大きいことを示す指標

Week4 : 相関と時系列

中山厚穂氏（首都大学東京大学院社会科学研究科　准教授）

4-1. 相関と散布図

プロモーション活動の広告費と売上のデータ
- 広告費と売上の関係を視覚的に捉えるために使われるのが「散布図」
- 「説明変数」を横軸に、「目的変数」を縦軸に据える

4-2. 層別散布図

グループの情報が得られるときには、グループごとに散布図を描くと有効な場合がある
- 層別をする
- 小学生の50m層のタイムと漢字書き取り能力のデータ（学年で層別する）
- 販売価格と販売数量のデータ（特別陳列の有無で層別する）
事前層別：確証的データ分析
- 事前に研究仮説があり、それをもとにデータ分析を通して確認するアプローチ
事後層別：探索的データ分析
- ビッグデータのように仮説の見当がぼんやりとしか分からないとき
- 分析を試行錯誤することでデータの真実を見つける

4-3. 相関係数

広告費と売上の関係性はどの程度のものか？
相関係数 r
- 相関の正負の方向とその強さを表す指標

${ \displaystyle r=\frac{\frac{1}{n}\Sigma(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sqrt{\frac{1}{n}\Sigma(x_{i}-\overline{x})^2}\sqrt{\frac{1}{n}\Sigma(y_{i}-\overline{y})^2}} }$

分母は2変数の標準偏差の積で、分子である共分散の単位を打ち消す働きもしている（データの変動の大きさも打ち消している）
共分散は、Xの平均偏差（平均との偏差）とYの平均偏差の積の和をデータの数で割ったもの
- 散布図で、広告費と売上のそれぞれの平均でグラフを4分割したときに、右上がりの領域（ともに平均よりも上、およびともに平均よりも下）のデータでは、偏差積の値が正になる
相関係数の範囲は、-1≦r≦1
- 0の場合は「無相関」とも呼ばれる
相関係数の評価の目安
- 0.0 ≦ |r| ≦ 0.2 ：ほとんど相関が無い
- 0.2 ＜ |r| ≦ 0.4 ：弱い相関
- 0.4 ＜ |r| ≦ 0.7 ：中程度（比較的強い）の相関
- 0.7 ≦ |r| ≦ 1.0 ：強い相関

4-4. 見かけの相関

疑似相関
- 第3の変数の影響により、2つの変数間の相関係数が見かけ以上に大きくなる
疑似無相関
- 第3の変数の影響により、2つの変数間の相関係数が見かけ上は相関が無くなる
2012年度プロ野球セリーグの個人打撃成績
- 安打と四球の相関係数・・・r=0.851
- 安打と三振の相関係数・・・r=0.156
  - 打席数という第3の変数が影響しているのでは？
偏相関係数
- 第3の変数の影響を取り除いた相関係数

${ \displaystyle r_{XY|Z}=\frac{r_{XY}-r_{XZ}r_{ZY}}{\sqrt{(1-r_{XZ}^2)(1-r_{ZY}^2)}} }$

4-5. 相関と時系列

相関係数はあくまで直線的な関連性を捉えている
- 非線形関係（曲線的な関係）は相関係数では捉えることができない
相関係数は外れ値の影響を受ける
- よって、散布図も同時に活用するのが正しいやり方
相関係数を解釈するときのその他の注意点
床面効果
- 試験内容が難しすぎて0点付近に多数が分布してしまうケース（最低点が0点に制限されてなければ測定できたかもしれない能力が測れない）
天井効果
- 試験内容が簡単すぎるため、最高得点に多数が分布してしまうケース
切断効果
- 偏った範囲のデータしか得られていない場合
- 入学試験の得点と入学後の成績（受験者の選抜により不合格者のデータが補足できず、正しい相関が見られない）

4-6. 単回帰分析

回帰分析
- 直線により表現される説明変数から目的変数の値を予測式を求める
- 説明変数が1つの場合、単回帰分析
- 説明変数が複数ある場合は、重回帰分析
最小二乗法
- Y軸方向の誤差を最小にする（正と負の誤差が存在するので二乗和を計算する）
決定係数
- 目的変数の変動のうち、説明変数によって説明される部分の割合
- 0.7〜0.8程度であれば当てはまりが良いとされる

4-7. 時系列グラフ、移動平均

時系列データ
- 時間軸上で等間隔に観測される系列的なデータ
- 等間隔にデータが記録されていることが重要
読み取るべき特徴
- 長期的な傾向（トレンド）：右肩上がり、右肩下がり
- 周期性
- ノイズ：不規則な変化
魚介類の1世帯当たり年平均1ヶ月間の支出金額
移動平均
- データを平滑化（滑らかにする）
- 周期性をならす
  - 季節周期の平滑化（12ヶ月移動平均を取ることで季節の周期を均す）
  - 曜日周期の平滑化（7日移動平均を取ることで曜日の周期を均す）
  - 日周期の平滑化（24時間移動平均を取ることで1日の周期を均す）
- 不規則な値の変化を打ち消す
- 東京都の年平均気温（平均気温、5年移動平均、15年移動平均）
平均をとる期間を長くすればするほど、より長期の傾向を示す

4-8. 指数、増加（減少)率、成長率

時間系列に沿ってデータの変動の特徴を読み取る
様々な加工により、変化が分かりやすくなる
- 指数
- 増加（減少）率
- 成長率
指数

${ \displaystyle 指数=\frac{比較時点tの値}{基準点t_{0}の値}\times 100 }$

増加（減少）率

${ \displaystyle 比較時点(t)での増加（減少）率=\frac{比較時点tの値-基準点t_{0}の値}{基準点t_{0}の値} }$

成長率

${ \displaystyle 比較時点(t)での成長率=\frac{比較時点tの値-比較時点の一時点前t_{-1}の値}{比較時点の一時点前t_{-1}の値} }$

Week5: 公的統計の活用とまとめ

奥田直彦氏（総務省統計局統計情報システム課長）

5-1. 統計調査の役割

e-Stat
母集団
- 調べたい対象全体からなる集団
標本
- 母集団から一部を抜き出したもの
全数調査
- 国勢調査（母集団は日本の世帯全体）
- 経済センサス（母集団は日本の事業所全体）
標本調査
標本抽出法
- 無作為抽出
  - ランダム・デジット・ダイヤリング
- 層化抽出

5-2. 公的統計制度の仕組み

分散型統計機構
- 国の行政機関がそれぞれ所管する行政分野に関する統計を作成する
総務省統計局
- 国勢調査や経済センサスなど最も基本的かつ重要な統計や、CPI、労働力調査、家計調査など主要な経済指標となる統計の作成等を担う中央統計期間

5-3. 統計情報の加工・提供

統計情報の発信、高度利用の促進、統計（データ）リテラシーの普及・啓発
統計局ホームページ
総合統計書
- 日本統計年鑑
- 日本の統計
- Statistical Handbook of Japan
- 世界の統計
- 統計でみる都道府県・市区町村のすがた（社会・人口統計体系）
地域メッシュ統計
- - 都市計画や防災計画の策定、民間企業が出店する際の商圏分析などで幅広く利用される
政府統計の総合窓口（e-Stat）
- 政府統計のポータルサイト

5-4. e-Statの紹介

e-Stat
「政府統計共同利用システム」として平成20年に開発
主な機能
- 統計表のダウンロード
- 統計データベース
  - 国勢調査等の主要な統計表については、データベース化。グラフ化も可能
- 都道府県・市区町村のすがた（地域統計概観）
- 統計GIS
活用方法

5-5. e-Statの使い方（人口ピラミッドの作成）

http://www.e-stat.go.jp/estat/guide/instructions/03/

5-6. e-Statの使い方（統計GIS）

http://e-stat.go.jp/SG2/eStatFlex/

5-7. 新たな取組の紹介

統計力向上サイト「データサイエンス・スクール」
- 社会人、ビジネスパーソンを対象
アプリDe統計
- City Stat
- ポケット統計
- とうけいどけい

5-8. 標本誤差と確率

標本誤差
- 標本から得られた結論に伴う確率的な誤差
- 確率論や統計的推測から、標本誤差を見積もることが重要
- 台風の予報円の定義は「円内に台風の中心が入る確率が70％」
信頼係数95％の信頼区間
- アメリカでは、世論調査の結果を示す際に「margin of error」として示される
- 生物的な実験の結果を表示する際には、エラーバー（誤差範囲）を付ける

5-9. まとめと更なる学習

反転授業（2014.12.20）

グループディスカッション

シンプソンのパラドックス
- 男性の新規顧客数 31と比較して、女性が 390と大きいために、女性の影響が大きく繁栄されてしまっているのが原因

第3の変数を見抜くには
- 計測可能な項目を経験上把握しておいて、統計調査の段階でデザインに組み込んでおく必要がある

他のグループの発表

唐揚げ定食だったら、（年配の人は唐揚げを食べないだろうから）「年齢」を考慮すべきでは？
今回の例では、「打席数」を第3の変数として偏相関係数を取るのではなく、「打率」と「三振率」で相関を取るとよかったのでは？

その他

「影響を取り除く」と「影響をコントロール」は同じ意味

R 演習

反転授業には Mac を持っていったのですが、R Console (on Mac) で日本語文字化け問題がいろいろと。

1. Mac で日本語の入ったCSVを読み込むとエラーが出る場合のおまじない

read.csv("xxx.csv", fileEncoding="cp932")

2. Quarzで日本語文字化け

> cm <- c(268.8, 252.1, 300.7, 206.8, 280.4, 172.7, 244.6, 212.4, 265.5, 153.6, 225.0)
> sales <- c(3233.5, 2814.7, 4605.4, 2859.7, 4155.7, 2062.6, 2587.0, 2254.8, 3655.8, 1483.5, 3412.1)
> data1 <- data.frame(広告費=cm, 売上=sales)
> par(mfrow=c(2, 2))
> hist(data1$広告費)

のように、日本語をラベルにすると文字化けしてしまう。

f:id:akiyoko:20141228105546p:plain

うまくいった対策例がこちら ↓

<a href="http://cortyuming.hateblo.jp/entry/20140619/p3"> RStudio for MacOSX でプロットが文字化けする場合のメモ - 牌語備忘録 -pygo</a>

~/.Rprofile

setHook(packageEvent("grDevices", "onLoad"),
        function(...){
          if(.Platform$OS.type == "windows")
            grDevices::windowsFonts(sans ="MS Gothic",
                                    serif="MS Mincho",
                                    mono ="FixedFont")
          if(capabilities("aqua"))
            grDevices::quartzFonts(
                sans =grDevices::quartzFont(
                    c("Hiragino Kaku Gothic Pro W3",
                      "Hiragino Kaku Gothic Pro W6",
                      "Hiragino Kaku Gothic Pro W3",
                      "Hiragino Kaku Gothic Pro W6")),
                serif=grDevices::quartzFont(
                    c("Hiragino Mincho Pro W3",
                      "Hiragino Mincho Pro W6",
                      "Hiragino Mincho Pro W3",
                      "Hiragino Mincho Pro W6")))
          if(capabilities("X11"))
            grDevices::X11.options(
                fonts=c("-kochi-gothic-%s-%s-*-*-%d-*-*-*-*-*-*-*",
                    "-adobe-symbol-medium-r-*-*-%d-*-*-*-*-*-*-*"))
          grDevices::pdf.options(family="Japan1GothicBBB")
          grDevices::ps.options(family="Japan1GothicBBB")
        }
        )
attach(NULL, name = "JapanEnv")
assign("familyset_hook",
       function() {
         winfontdevs=c("windows","win.metafile",
             "png","bmp","jpeg","tiff","RStudioGD")
         macfontdevs=c("quartz","quartz_off_screen","RStudioGD")
         devname=strsplit(names(dev.cur()),":")[[1L]][1]
         if ((.Platform$OS.type == "windows") &&
                 (devname %in% winfontdevs))
           par(family="sans")
         if (capabilities("aqua") &&
                 devname %in% macfontdevs)
           par(family="sans")
       },
       pos="JapanEnv")
setHook("plot.new", get("familyset_hook", pos="JapanEnv"))
setHook("persp", get("familyset_hook", pos="JapanEnv"))

本題

> # 広告費
> cm <- c(268.8, 252.1, 300.7, 206.8, 280.4, 172.7, 244.6, 212.4, 265.5, 153.6, 225.0)
> # 売上
> sales <- c(3233.5, 2814.7, 4605.4, 2859.7, 4155.7, 2062.6, 2587.0, 2254.8, 3655.8, 1483.5, 3412.1)
> data1 <- data.frame(広告費=cm, 売上=sales)
> data1
   広告費   売上
1   268.8 3233.5
2   252.1 2814.7
3   300.7 4605.4
4   206.8 2859.7
5   280.4 4155.7
6   172.7 2062.6
7   244.6 2587.0
8   212.4 2254.8
9   265.5 3655.8
10  153.6 1483.5
11  225.0 3412.1

ヒストグラム

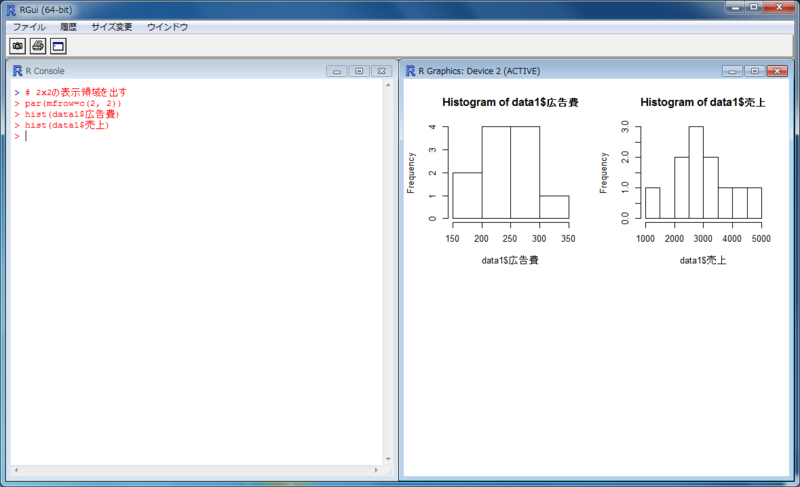
> # 2x2の表示領域を出す
> par(mfrow=c(2, 2))
> hist(data1$広告費)
> hist(data1$売上)

f:id:akiyoko:20141228033057p:plain

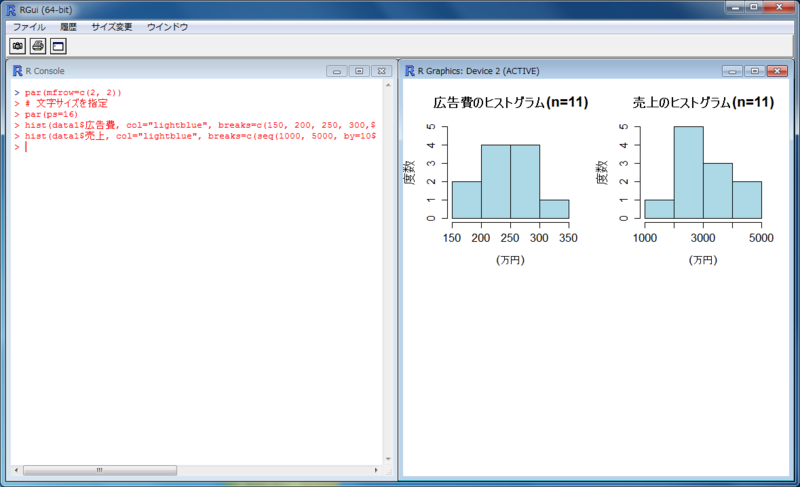
装飾いろいろ

> par(mfrow=c(2, 2))
> # 文字サイズを指定
> par(ps=16)
> hist(data1$広告費, col="lightblue", breaks=c(150, 200, 250, 300, 350), ylim=c(0, 5), xlab="(万円)", ylab="度数", main="広告費のヒストグラム(n=11)")
> hist(data1$売上, col="lightblue", breaks=c(seq(1000, 5000, by=1000)), ylim=c(0, 5), xlab="(万円)", ylab="度数", main="売上のヒストグラム(n=11)")

f:id:akiyoko:20141228033106p:plain

回帰分析

> par(mfrow=c(2, 2))
> plot(売上 ~ 広告費, data=data1)
> result <- lm(formula=売上 ~ 広告費, data=data1)
> # 回帰直線
> abline(result)
> summary(result)

Call:
lm(formula = 売上 ~ 広告費, data = data1)

Residuals:
    Min      1Q  Median      3Q     Max
-602.87 -372.99   85.91  336.01  578.62

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept) -1257.663    712.937  -1.764 0.111547
広告費         18.183      2.986   6.089 0.000182 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 430.1 on 9 degrees of freedom
Multiple R-squared:  0.8047,    Adjusted R-squared:  0.783
F-statistic: 37.08 on 1 and 9 DF,  p-value: 0.0001815

> # 相関係数
> cor(data1)
          広告費      売上
広告費 1.0000000 0.8970485
売上   0.8970485 1.0000000

f:id:akiyoko:20141228033941p:plain

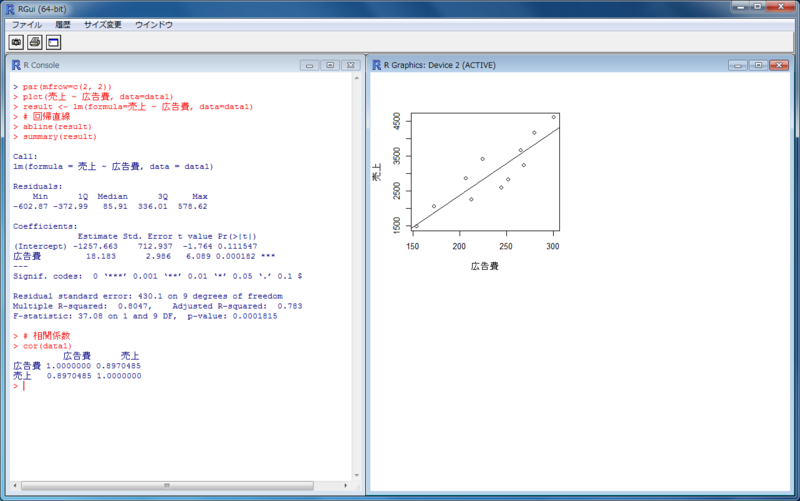
装飾いろいろ

> par(mfrow=c(2, 2))
> par(ps=16)
> plot(売上 ~ 広告費, data=data1, pch=21, col="red", bg="red", cex=1.5, xlab="広告費(万円)", ylab="売上(万円)", main="広告費と売上の産婦図と\n回帰直線")
> result <- lm(formula=売上 ~ 広告費, data=data1)
> abline(result, col="blue", lwd=3)

> # テキスト
> text(160, 4000, "y=-1257.66+18.18x", adj=0)
> text(260, 2000, "r=0.897", adj=0)

f:id:akiyoko:20141228033749p:plain

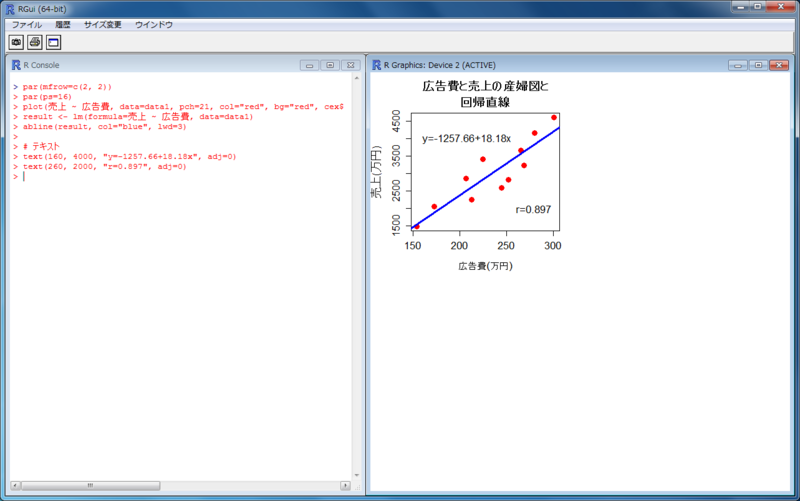
残差分析

> 残差 <- residuals(result)
> data_res <- cbind(data1, 残差)
> data_res
   広告費   売上       残差
1   268.8 3233.5 -396.39377
2   252.1 2814.7 -511.53977
3   300.7 4605.4  395.47255
4   206.8 2859.7  357.14442
5   280.4 4155.7  314.88489
6   172.7 2062.6  180.08043
7   244.6 2587.0 -602.86822
8   212.4 2254.8 -349.57967
9   265.5 3655.8   85.90971
10  153.6 1483.5  -51.72668
11  225.0 3412.1  578.61611

> par(mfrow=c(2, 2))
> plot(残差 ~ 広告費, data=data_res, pch=21, col="red", bg="red", cex=1.5, ylim=c(-1500, 1500), xlab="広告費(万円)", ylab="残差(万円)", main="残差分析")
> abline(h=0)

f:id:akiyoko:20141228033149p:plain

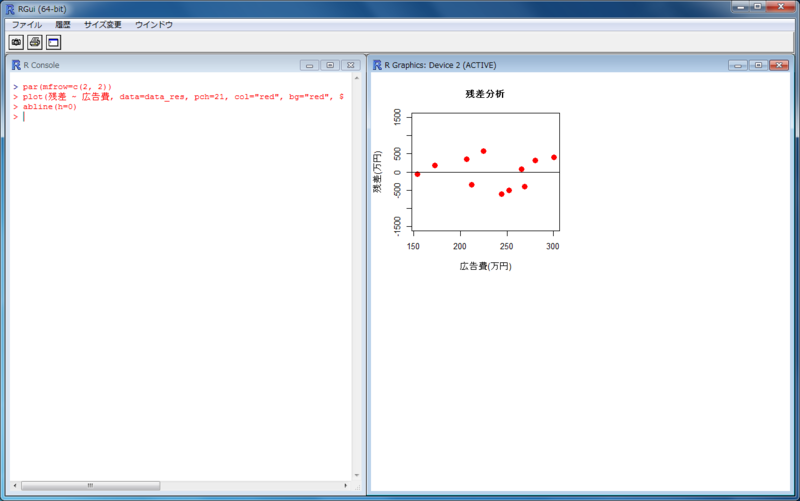
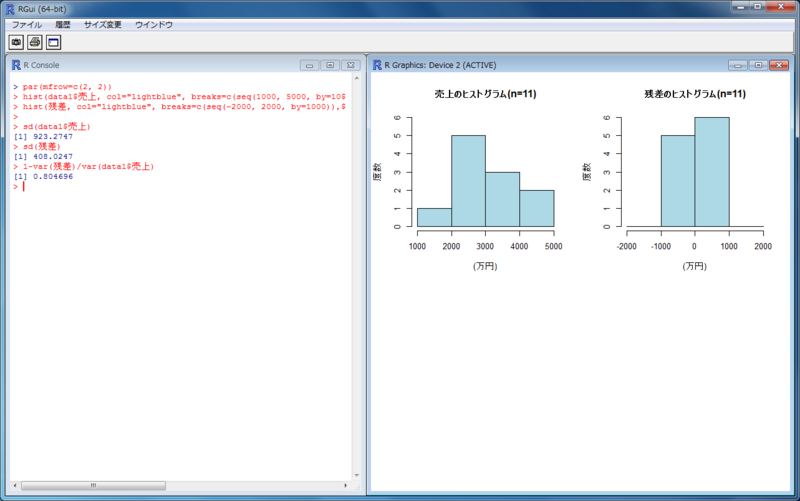
決定係数R2の意味

> par(mfrow=c(2, 2))
> hist(data1$売上, col="lightblue", breaks=c(seq(1000, 5000, by=1000)), ylim=c(0, 6), xlab="(万円)", ylab="度数", main="売上のヒストグラム(n=11)")
> hist(残差, col="lightblue", breaks=c(seq(-2000, 2000, by=1000)), ylim=c(0, 6), xlab="(万円)", ylab="度数", main="残差のヒストグラム(n=11)")
> 
> sd(data1$売上)
[1] 923.2747
> sd(残差)
[1] 408.0247
> 1-var(残差)/var(data1$売上)
[1] 0.804696